二叉树与递归有着千丝万缕的联系,二叉树在定义时就使用了递归的概念:一棵二叉树可能是空树,如果不是空树,那么它的左右子树都是二叉树。
1 | // 二叉树 |
基础:二叉树的遍历
遍历时均无返回值,所以遍历要另写函数,把需要返回的作为参数传入。
DFS, 深度优先
先序遍历:根左右(文件目录结构)
常规迭代
- 初始化栈,并将根节点入栈;
- 当栈不为空时:
- 弹出栈顶元素 node,并将值添加到结果中;
- 如果 node 的右子树非空,将右子树入栈;
- 如果 node 的左子树非空,将左子树入栈;
由于栈是“先进后出”的顺序,所以入栈时先将右子树入栈,这样使得前序遍历结果为 “根->左->右”的顺序。

1 | // 迭代,非递归实现,本质使用栈模拟递归 |
模板迭代
- 先将根节点
cur和所有的左孩子入栈并加入结果中,直至cur为空 - 每弹出一个栈顶元素
tmp,就到达它的右孩子,再将这个节点当作cur重新按上面的步骤来一遍,直至栈为空。
1 | public void preorderTraversal(TreeNode root) { |
1 | // 递归实现 |
中序遍历:左根右
模板迭代:
- 先将根节点
cur和所有的左孩子入栈中,直至cur为空 - 每弹出一个栈顶元素
tmp,加入结果中,并到达它的右孩子,再将这个节点当作cur重新按上面的步骤来一遍,直至栈为空。
1 | public void preorderTraversal(TreeNode root) { |
1 | // 递归实现 |
后续遍历:左右根
对前序遍历的(根左右)修改为(根右左),再倒序输出。
1 | // 常规倒序输出 |
1 | // 递归实现 |
BFS, 广度优先(层次遍历)
广度优先搜索的步骤为:
- 初始化队列 q,并将根节点 root 加入到队列中;
- 当队列不为空时:
- 队列中弹出节点 node,加入到结果中;
- 如果左子树非空,左子树加入队列;
- 如果右子树非空,右子树加入队列;
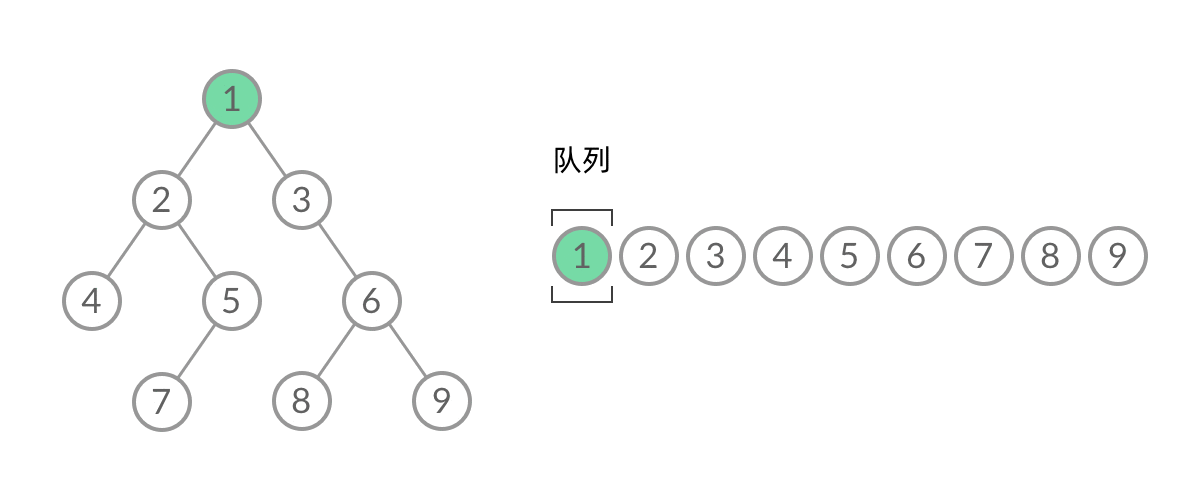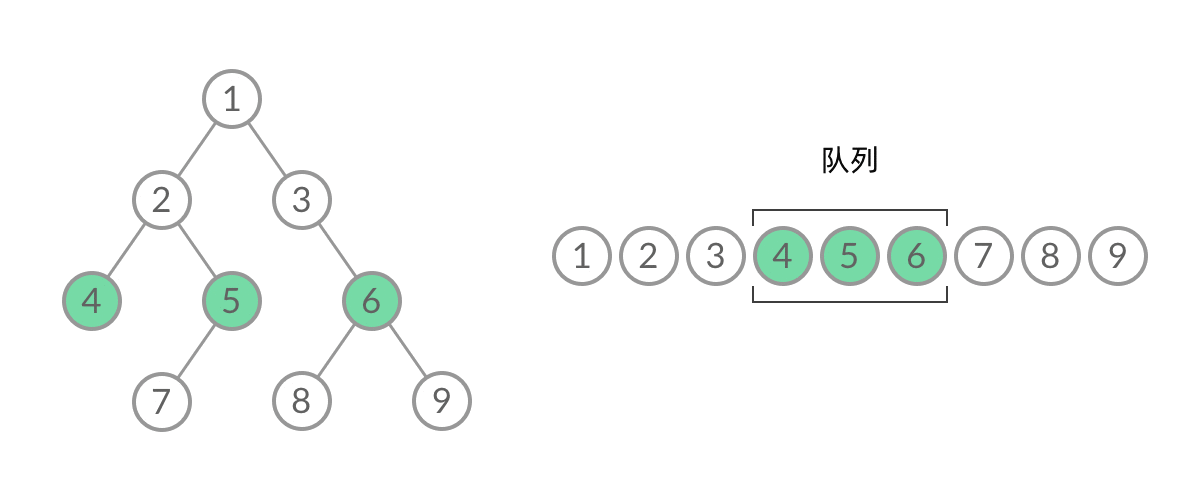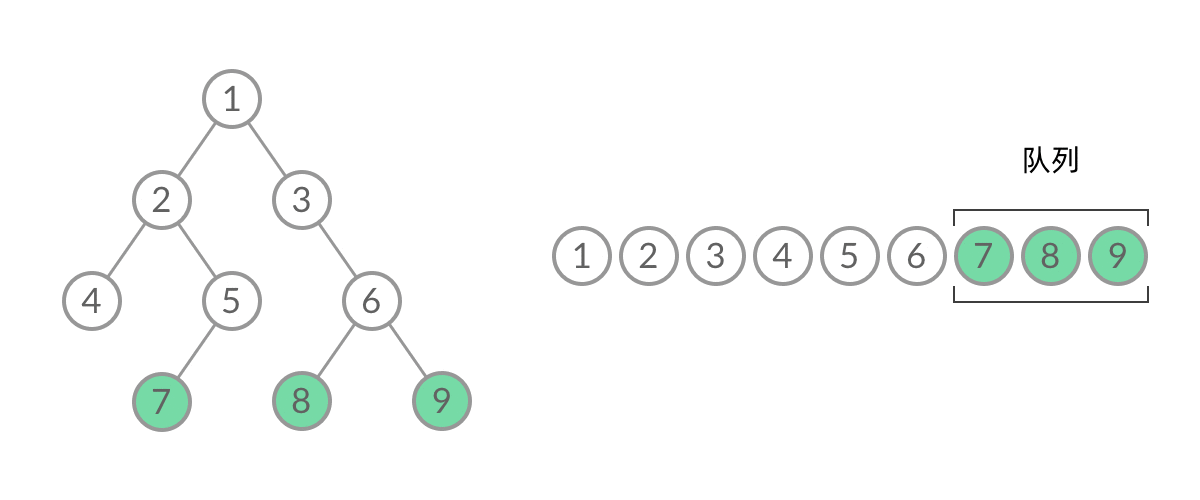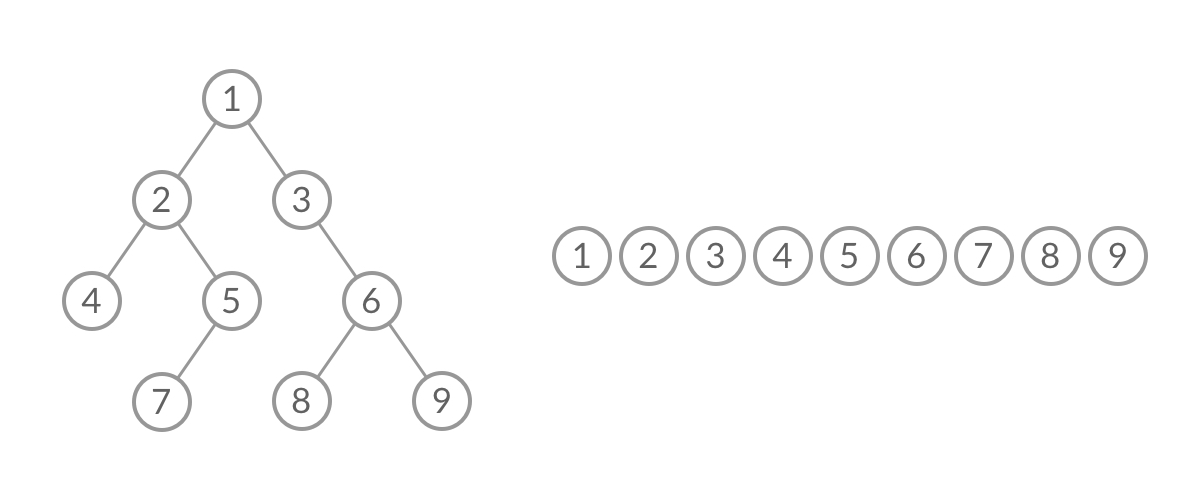
1 | //队列实现,分层次,在每一层遍历开始前,先记录队列中的结点数量 n(也就是这一层的结点数量),然后一口气处理完这一层的 n 个结点。 |
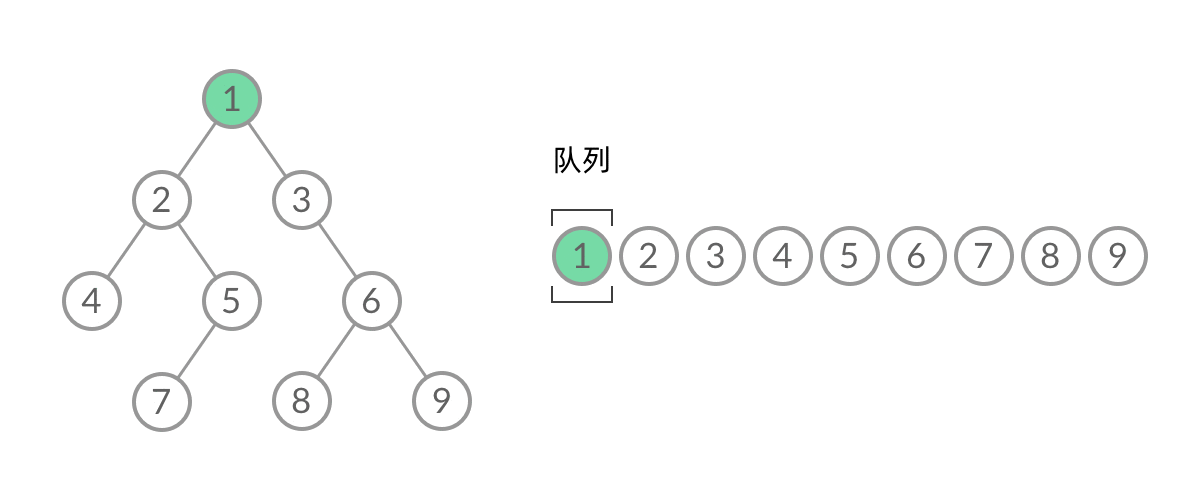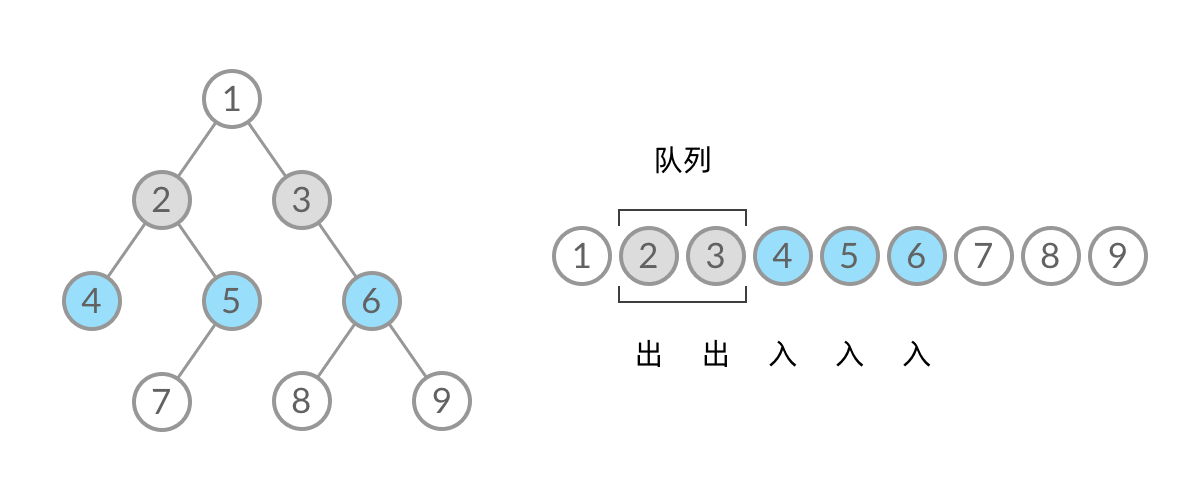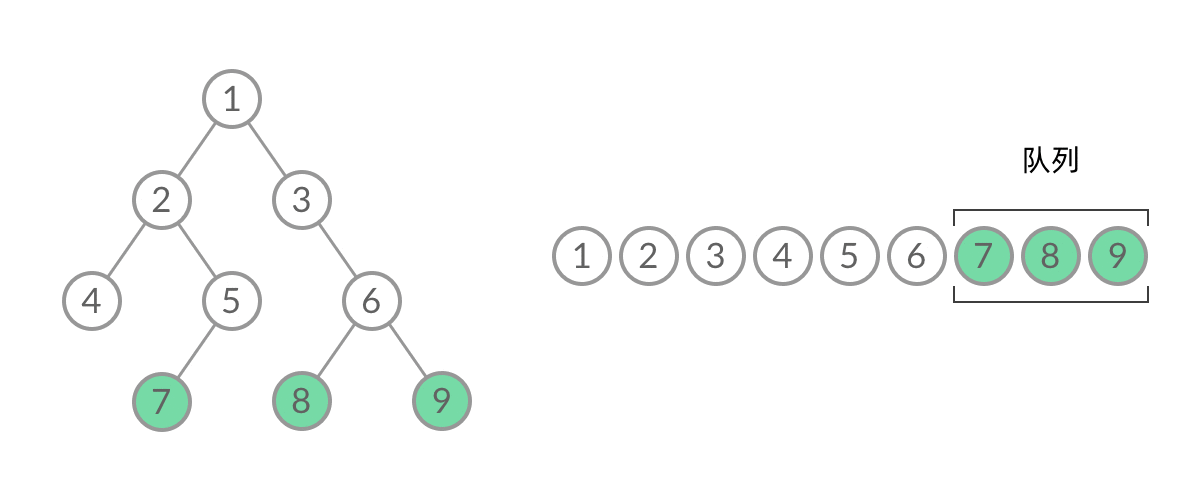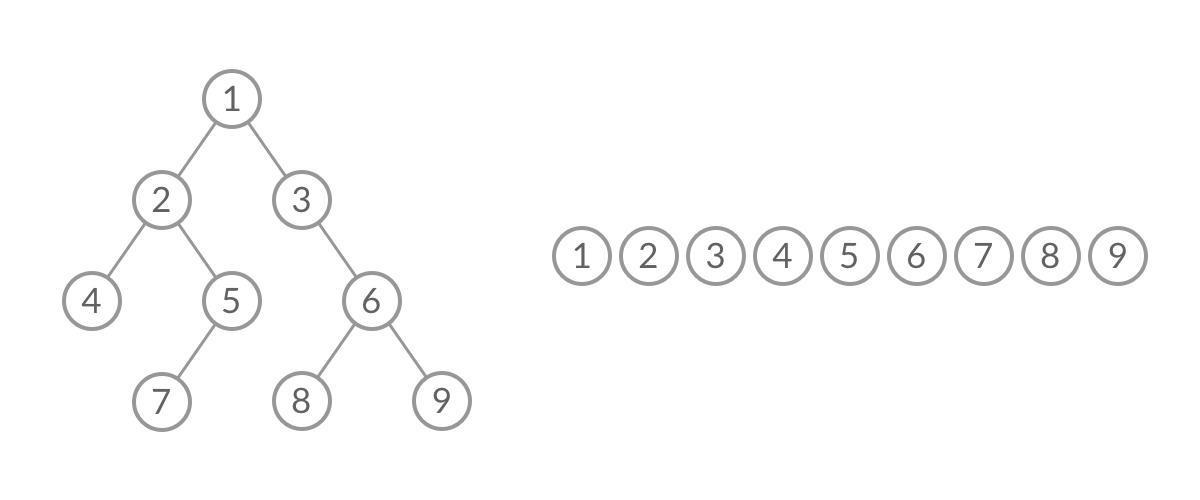
BFS常用于找最短路径。
在一棵树中,一个结点到另一个结点的路径是唯一的,但在图中,结点之间可能有多条路径,其中哪条路最近?这一类问题称为最短路径问题。最短路径问题也是 BFS 的典型应用,而且其方法与层序遍历关系密切。
在二叉树中,BFS 可以实现一层一层的遍历。在图中同样如此。从源点出发,BFS 首先遍历到第一层结点,到源点的距离为 1,然后遍历到第二层结点,到源点的距离为 2…… 可以看到,用 BFS 的话,距离源点更近的点会先被遍历到,这样就能找到到某个点的最短路径了。
表达式树:分别对应前缀表达式/中缀表达式/后缀表达式
树叶是操作数值,其他节点是操作符。
后缀表达式转树:操作数压栈,操作符弹栈
对应例题
先序遍历
144 二叉树的先序遍历
589 N 叉树的前序遍历
606 根据先序遍历结果构造字符串
- 在先序遍历中,对每个非空访问元素,在进行处理时,先形成字符串”(“+ root.val;
例如,对于[1,2,3,4],得到”(1(2(4”
- 如果当前访问的节点的左子树为空且右子树不为空,就在字符串中添加一个”()”
这样得到, “(1(2(4()”- 同时,对于每轮递归中,在最终返回前,补全右括号”)”
这样得到 “(1(2(4())(3))”
由此,基本输出形式已经完成。剩下处理头尾两个多余括号。331 验证是否是合法先序遍历结果
- 二叉树看成有向图,一条有向边带来一个入度和一个出度,二叉树的总入度等于总出度,也等于边数。即,遍历到最后,总入度肯定等于总出度。
- 还没遍历到最后时,肯定不会出现 入度 >= 出度 的时刻。
提供 1 个出度可以理解为提供一个挂载点,提供 1 个入度为消耗一个挂载点。入度 >= 出度,意味着当前已遍历的节点,消耗的挂载点已经大于等于提供的挂载点。说明已经没法挂载接下来遍历的节点了,还有要挂的,但挂满了,是不合法的。
中序遍历
94 基本的中序遍历
173 二叉搜索树迭代器
中序遍历一般会和BST(二叉搜索树)结合使用,这样访问的顺序是升序
后序遍历
145 基本的二叉树的后序遍历
590 N 叉树的后序遍历
层序遍历
102 二叉树的层序遍历
103 二叉树的锯齿形层序遍历(每层加flag或用双端队列)
107 二叉树的层序遍历 II(自底向上)
429 N 叉树的层序遍历
树的基本操作
递归三步:确定递归函数的参数和返回值;确定终止条件(if(root == null) return;);确定单层递归逻辑(对哪个节点进行什么递归操作);
226 翻转二叉树(对于每个节点,交换其左右子树,递归其左右子树)
100 相同的树(对于每个节点,判断其值是否相等,递归其左右子树)
572 另一个树的子树(一个树是另一个树的子树,要么这两个树相等;要么这个树是左树的子树;要么是右树的子树。)
剑指 Offer 26 树的子结构
- 先序遍历树 A中的每个节点;(对应函数
isSubStructure(A, B))
- 特例处理: 当 树 A为空 或 树 B 为空 时,直接返回 false;
- 返回值: 若树 BB 是树 AA 的子结构,则必满足以下三种情况之一,因此用或 || 连接;
以 节点 A为根节点的子树 包含树 B ,对应recur(A, B);
树 B 是 树 A 左子树 的子结构,对应isSubStructure(A.left, B);
树 B 是 树 A 右子树 的子结构,对应isSubStructure(A.right, B);- 判断树A中 以当前节点为根节点的子树 是否包含树B。(对应函数
recur(A, B))
- 终止条件:
当节点 B 为空:说明树 B 已匹配完成(越过叶子节点),因此返回 true ;
当节点 A 为空:说明已经越过树 A 叶子节点,即匹配失败,返回 false ;
当节点 A 和 B 的值不同:说明匹配失败,返回 false ;- 返回值:
判断 A 和 B 的左子节点是否相等,即recur(A.left, B.left);
判断 A 和 B 的右子节点是否相等,即recur(A.right, B.right);
101 对称二叉树/剑指 Offer 28(添加辅助函数,对于每个节点的左右孩子,判断其左的右和右的左,左的左和右的右是否相等,递归其左的右和右的左,左的左和右的右)
617 合并二叉树
965 单值二叉树
104 二叉树的最大深度/559 N 叉树的最大深度/111 二叉树的最小深度/110 平衡二叉树(一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 )
257 二叉树的所有路径
二叉搜索树(BST)
基础操作:创建,判断 BST 的合法性、增、删、查。删较复杂
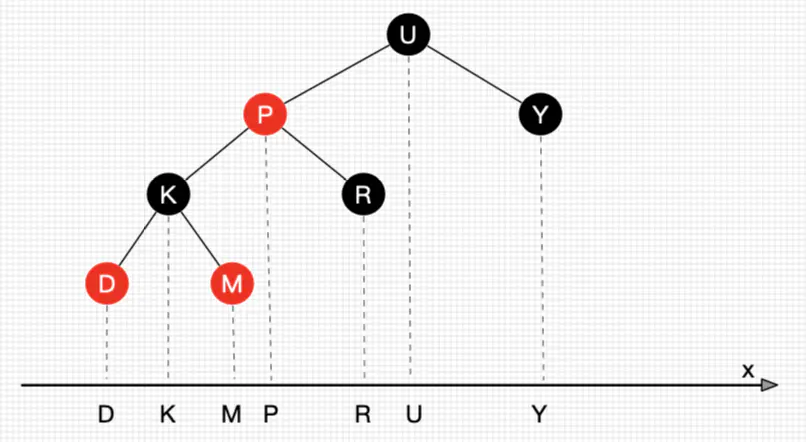
性质:中序遍历为升序/投射x轴后有序。
创建
95 不同的二叉搜索树 II
108 将有序数组转换为二叉搜索树
109 有序链表转换二叉搜索树
合法性
98 验证二叉搜索树(中序遍历为升序/左子树不空,左子树上所有节点的值均小于根节点的值; 若右子树不空,则右子树上所有节点的值均大于根节点的值;左右子树也为二叉搜索树。)
剑指33 判断数组是不是某二叉搜索树的后序遍历结果
查
700 二叉搜索树中的搜索
增
701 二叉搜索树中的插入操作
删(合并删除/排序删除)
450.删除二叉搜索树中的节点
合并删除:实质是将被删节点的的左子树合并到右子树上(反之也可),导致树的高度发生变化,极其容易导致树结构的不平衡。
- 没找到删除的节点,遍历到空节点直接返回
找到删除的节点
- 左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
- 删除节点的左孩子为空,右孩子不为空,删除节点,右孩子补位,返回右孩子为根节点
- 删除节点的右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
- 左右孩子节点都不为空,则将删除节点左孩子放到删除节点的右子树的最左面节点的左孩子上,返回删除节点右孩子。
2
3
4
5
6
7
8
TreeNode cur = root.right;
while(cur.left != null){
cur = cur.left;
}
cur.left = root.left;
root = root.right;
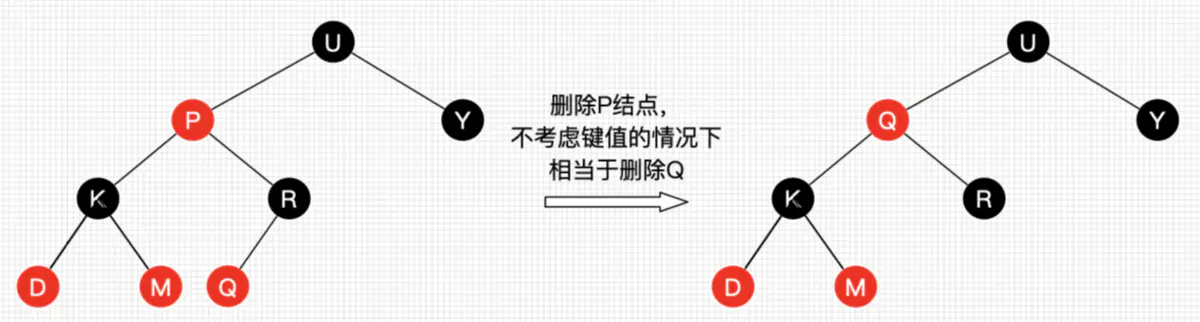
return root;复制删除:不删除这个结点,而是让这个节点被覆盖。没有改变树的深度,对于树的删除是更优。
后继节点:大于删除结点的最小结点(删除结点的右子树最左结点)
前驱节点:小于删除结点的最大结点(删除结点的左子树最右结点)
即中序遍历后被删节点的前驱和后继。
- 没找到删除的节点,遍历到空节点直接返回
找到删除的节点
- 左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
- 若删除结点只有一个子结点,用子结点替换删除结点
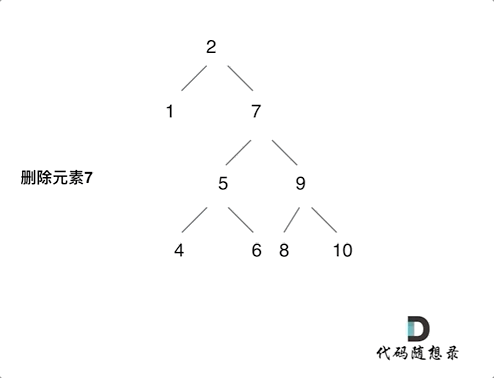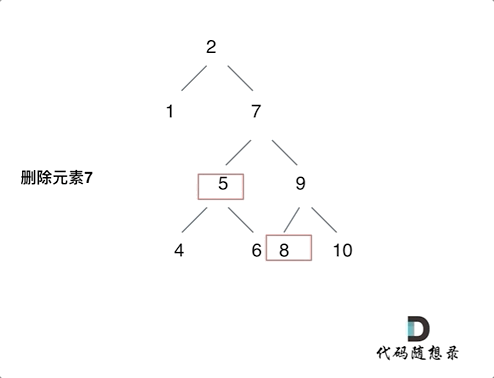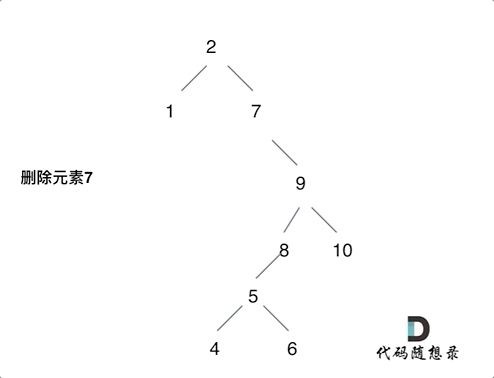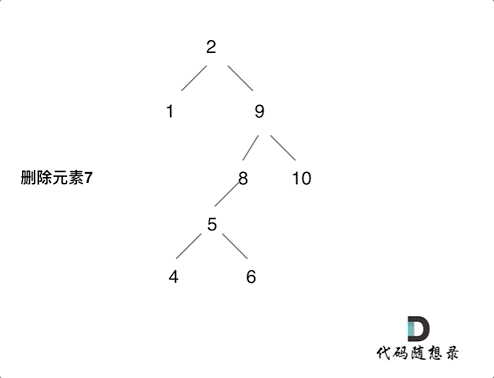
若删除结点有两个子结点,用后继结点替换删除结点(前驱结点替代也可以,但习惯上拿后继结点来替代),再删除该后继节点。
2
3
4
5
6
7
8
root = root.right;
while (root.left != null) root = root.left;
return root.val;
}
//删除结点有两个子结点的情况
root.val = successor(root); // 把 root.val 改成 successor
root.right = deleteNode(root.right, root.val); // 删除 successor
平衡二叉树(AVL树)
一个二叉查找树,每个节点的左右两个子树的高度差的绝对值不超过 1。
平衡因子: 某个结点的左子树的高度减去右子树的高度得到的差值。
why?
对于一般的二叉搜索树,其期望高度(即为一棵平衡树时)为$log_2n$,其各操作的时间复杂度$O(log_2n)$
但是,在某些极端的情况下(如在插入的序列是有序的时),二叉搜索树将退化成近似链或链,此时,其操作的时间复杂度将退化成线性的,即$O(n)$。
我们可以通过随机化建立二叉搜索树来尽量的避免这种情况,但是在进行了多次的操作之后,由于在删除时,我们总是选择将待删除节点的后继代替它本身,这样就会造成总是右边的节点数目减少,以至于树向左偏沉。这同时也会造成树的平衡性受到破坏,提高它的操作的时间复杂度。
例如:按顺序将一组数据{1,2,3,4,5,6}分别插入到一颗空二叉查找树和AVL树中,插入的结果如下图:
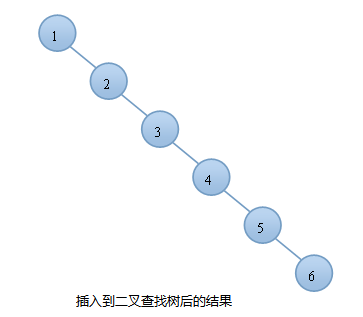
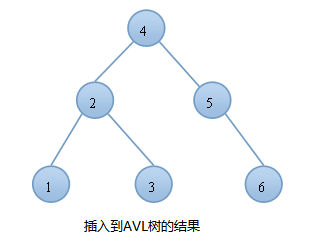
由图可知,同样的结点,由于插入方式不同导致树的高度也有所不同。
特别是在带插入结点个数很多且正序的情况下,会导致二叉树的高度是$O(N)$.
而AVL树就不会出现这种情况,树的高度始终是$O(logN)$。
how?
平衡化有两大基础操作: 左旋和右旋。这两种操作都是从失去平衡的最小子树根结点开始的(即离插入结点最近且平衡因子超过1的祖结点)。
左旋: y 结点变为该部分子树的根结点,同时 x 结点(连同其左子树 a)移动至 y 结点的左孩子。若 y 结点有左孩子 b,由于 x 结点需占用其位置,所以调整至 x 结点的右孩子处。
右旋:x 结点变为根结点,同时 y 结点连同其右子树 c 作为 x 结点的右子树,原 x 结点的右子树 b 变为 y 结点的左子树。
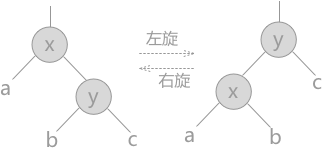
需要平衡的四种情况:(y为失衡节点)
- LL,向左子树(L)的左孩子(L)中插入新节点后导致不平衡。处理方法:右旋
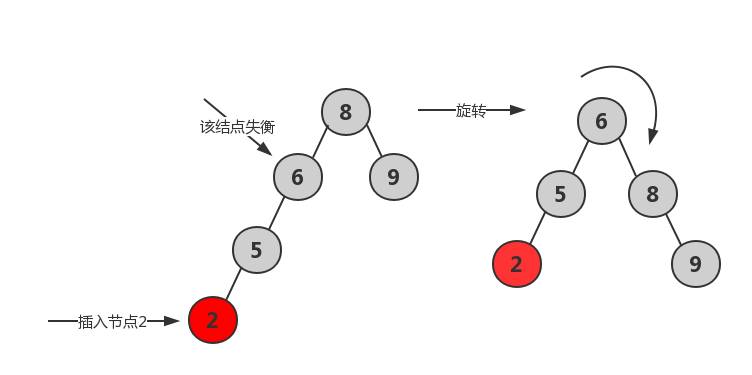
1 | //右旋转 |
- RR,向右子树(R)的右孩子(R)中插入新节点后导致不平衡。处理方法:左旋
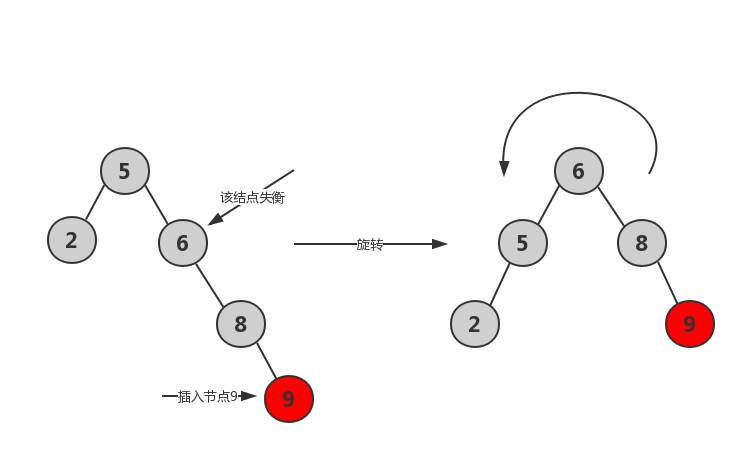
1 | //左旋转 |
- LR,处理方法:先左旋(变为LL情况)再右旋
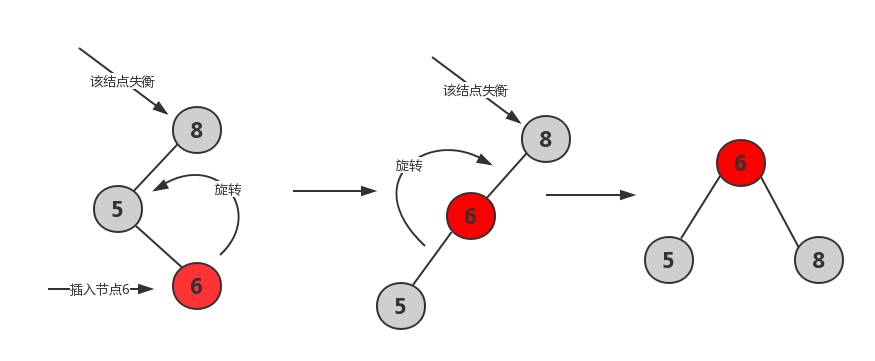
1 | //左右情况旋转 |
- RL,处理方法:先右旋(变为RR情况)再左旋
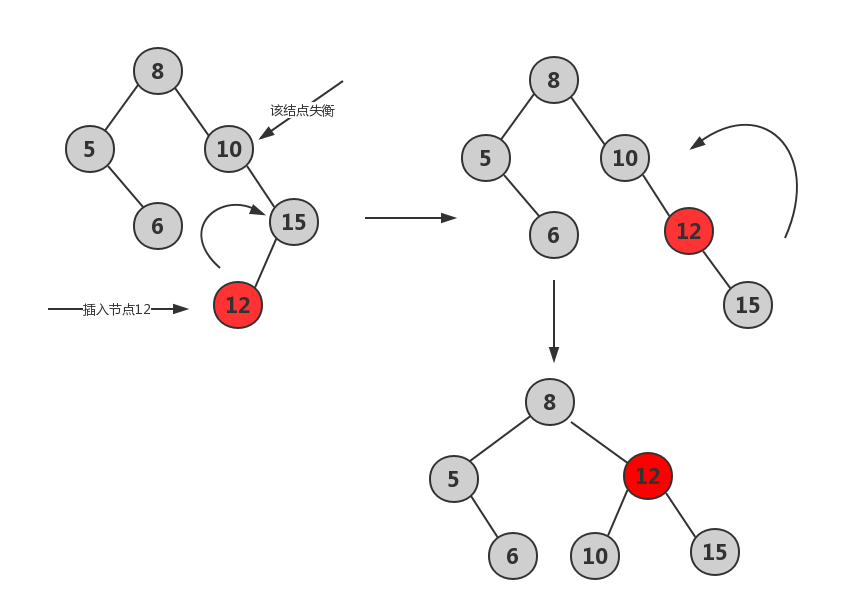
1 | //右左情况旋转 |
1 | public Node treeRebalance(Node root) { |
非旋转方法:二叉排序树 -> 中序遍历得升序数组 -> AVL树(leetcode 108)
可视化
AVL Tree Visualzation (usfca.edu)
红黑树(RBT)
红黑树本身是一棵二叉查找树,在其基础上附加了两个要求:
- 树中的每个结点增加了一个用于存储颜色的标志域;
- 树中没有一条路径比其他任何路径长出两倍,整棵树要接近于“平衡”的状态。
这里所指的路径,指的是从任何一个结点开始,一直到其子孙的叶子结点的长度;
接近于平衡:红黑树并不是平衡二叉树,只是由于对各路径的长度之差有限制,所以近似于平衡的状态。
红黑树节点属性:父节点,子节点(两个,左子节点和右子节点),颜色,value
树上的每个节点都遵循下面的规则:
- 每个节点都有红色或黑色
- 树的根始终是黑色的
- 每个叶子节点(NIL)是黑色。 [注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!]
- 没有两个相邻的红色节点(红色节点不能有红色父节点或红色子节点,并没有说不能出现连续的黑色节点)
- 从节点(包括根)到其任何后代NULL节点的每条路径都具有相同数量的黑色节点(即自平衡)
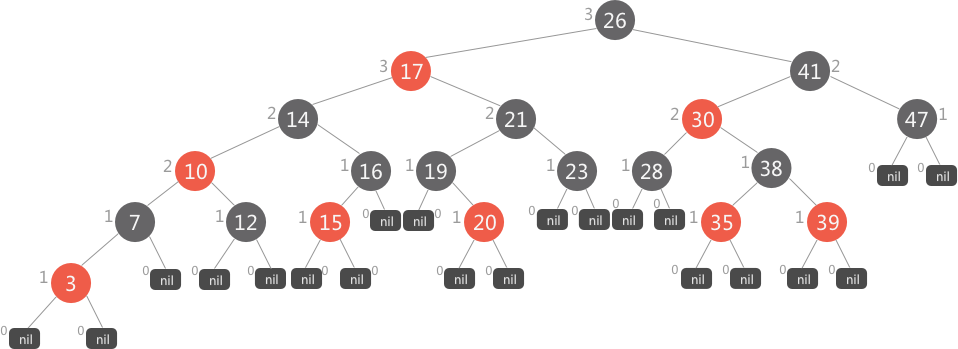
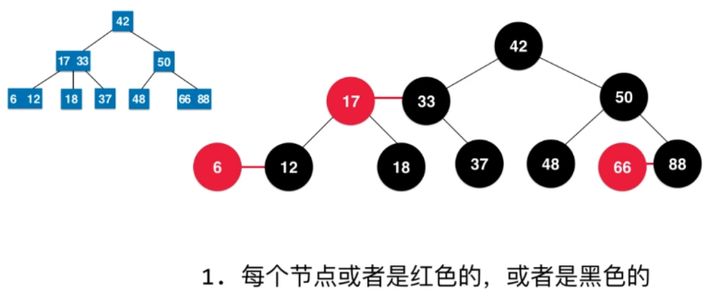
注意:图中每个结点附带一个整形数值,表示的是此结点的黑高度(从该结点到其子孙结点中包含的黑结点数,用 bh(x) 表示(x 表示此结点)),nil 的黑高度为 0,颜色为黑色(在编程时为节省空间,所有的 nil 共用一个存储空间)。在计算黑高度时,也看做是一个黑结点。
红黑树中每个结点都有各自的黑高度,整棵树也有自己的黑高度,即为根结点的黑高度,如图中的红黑树的黑高度为 3。对于一棵具有 n 个结点的红黑树,树的高度至多为:2lg(n+1)。
why?
对于高度为 h 的二叉查找树的运行时间为O(h),而包含有 n 个结点的红黑树本身就是最高为 lgn(简化之后)的查找树(h=lgn),所以红黑树的时间复杂度为O(lgn)。
红黑树,虽隶属于二叉查找树,但二叉查找树的时间复杂度会受到其树深度的影响,而红黑树可以保证在最坏情况下的时间复杂度仍为O(lgn)。当数据量多到一定程度时,使用红黑树比二叉查找树的效率要高。
相比于AVL树,牺牲了部分平衡性,以换取删除/插入操作时少量的旋转次数,整体来说,性能优于AVL树。
红黑树利用了缓存,等价于2-3树。
其中2-节点 等价于普通平衡二叉树的节点,3-节点 本质上是非平衡性的缓存。
要再平衡(rebalance)时,增删操作时,2-节点与3-节点的转化会吸收不平衡性,减少旋转次数,使再平衡尽快结束。在综合条件下,增删操作相当时,数据的随机性强时,3-节点的非平衡性缓冲效果越明显。因此红
黑树的综合性能更优。
本质上是用空间换时间。
查找方法同BST树。
基本操作
换色:即红变黑,黑变红,只需要让某个对象的属性改变
旋转,分为左旋和右旋,同二叉排序树转平衡二叉树的旋转原理完全相同。
插入节点
红黑树在插入数据时,插入的位置肯定在底部,不可能在中间突然插入一个值。
插入的数据一定是红色的(遵守红黑树规则5,如果有一条分支增加了一个黑色节点,就会打破该规则)
插入之后,为了满足规则4,就需要用到换色与左旋、右旋的操作
当创建一个红黑树或者向已有红黑树中插入新的数据时,执行以下 3 步:
- 按照二叉查找树插入结点的方法,找到新结点插入的位置;
- 将新插入的结点结点初始化,颜色设置为红色后插入到指定位置;
调整二叉查找树,想办法通过旋转以及修改树中结点的颜色,使其重新成为红黑树。分为以下情况:
- 插入位置为整棵树的树根。处理办法:将插入结点的颜色改为黑色。
- 插入位置的双亲结点的颜色为黑色。处理方法:此种情况不需要做任何工作
插入位置的双亲结点的颜色为红色。处理方法:此时需要结合其祖父结点和祖父结点的另一个孩子结点(父结点的兄弟结点,此处称“叔叔结点”)的状态,分为 3 种情况:
- 当前结点的父节点是红色,且叔叔结点也是红色:破坏了红黑树的第 4 条性质,解决方案为:将父结点颜色改为黑色;将叔叔结点颜色改为黑色;将祖父结点颜色改为红色;下一步将祖父结点认做当前结点,继续判断,处理结果如下图所示:
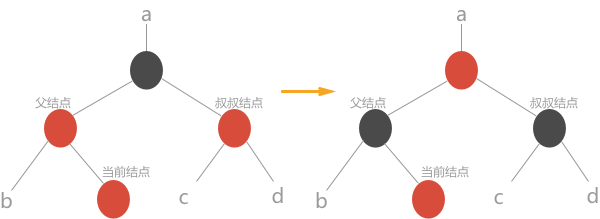
- 当前结点的父结点颜色为红色,叔叔结点颜色为黑色,且当前结点是父结点的右孩子。解决方案:将父结点作为当前结点做左旋操作,此种情况就转变成了第 3 种情况,处理过程转情况 3
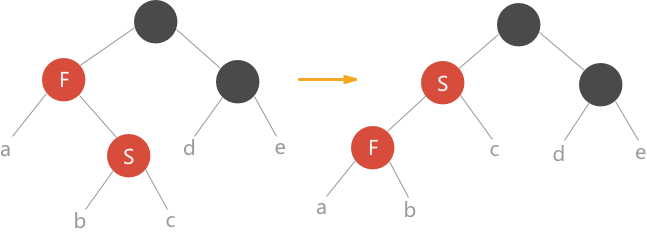
- 当前结点的父结点颜色为红色,叔叔结点颜色为黑色,且当前结点是父结点的左孩子。解决方案:将父结点颜色改为黑色,祖父结点颜色改为红色,从祖父结点处进行右旋处理。
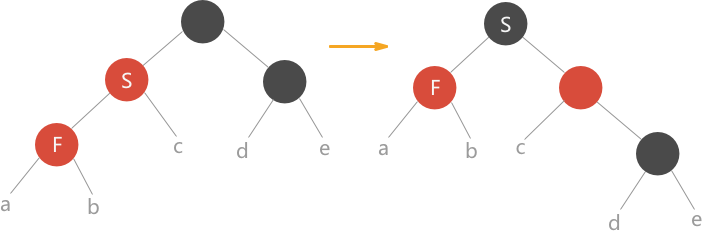
祖宗根节点必黑,允许黑连黑,不许红连红;新增红,爸叔通红就变色,爸红叔黑就旋转,哪黑往哪旋
删除节点
需要完成 2 步操作:
- 将红黑树按照BST删除结点的方法删除指定结点;
- 若该删除结点本身是叶子结点,则直接删除,返回NULL为根节点
- 若只有一个孩子结点(左孩子或者右孩子),则让其孩子结点顶替该删除结点;
- 若有两个孩子结点,则将删除节点左孩子放到删除节点的右子树的最左面节点的左孩子上,返回删除节点右孩子。
判断删除该结点是否会破坏红黑树的性质。判断的依据是:如果删除结点的颜色为红色,则不会破坏;如果删除结点的颜色为黑色,则破坏性质5,调整删除结点后的树,使之重新成为红黑树。调整方案分 4 种情况讨论
删除结点的兄弟结点颜色是红色,调整措施为:将兄弟结点颜色改为黑色,父亲结点改为红色,以父亲结点来进行左旋操作,同时更新删除结点的兄弟结点(左旋后兄弟结点发生了变化),如下图所示:

删除结点的兄弟结点及其孩子全部都是黑色的,调整措施为:将删除结点的兄弟结点设为红色,同时设置删除结点的父结点标记为新的结点,继续判断;

删除结点的兄弟结点是黑色,其左孩子是红色,右孩子是黑色。调整措施为:将兄弟结点设为红色,兄弟结点的左孩子结点设为黑色,以兄弟结点为准进行右旋操作,最终更新删除结点的兄弟结点;
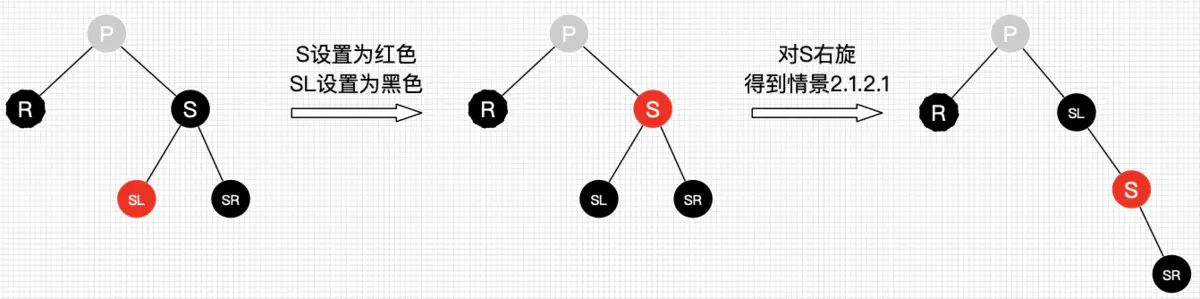
删除结点的兄弟结点是黑色,其右孩子是红色(左孩子不管是什么颜色),调整措施为:将删除结点的父结点的颜色赋值给其兄弟结点,然后再设置父结点颜色为黑色,兄弟结点的右孩子结点为黑色,根据其父结点做左旋操作,最后设置替换删除结点的结点为根结点;

应用
Java中TreeSet和TreeMap的实现,以及JDK 8以后,HashMap的设计