图与网络 / 贪心算法

贪心算法在对问题求解时，总是做出在当前看来是最好的选择。

最小生成树问题(Minimum spanning trees,MST)

生成树：指一个连通子图，它含有图中全部$n$个顶点，但只有足以构成一棵树的$n-1$条边。
最小生成树：在所有生成树中，所有边的权重和最小的生成树。
假设有一个连通的无向的图$G=(V,E)$，及权值函数$w: E\rightarrow R$。考虑贪婪的方法找出$MST$。

这个贪心策略由下面的“一般型”算法延伸，该算法每次只增长最小生成树的一条边。

该算法管理边集$A$，$A$不断加$1$条边，需要做$n-1$次循环。在每次迭代之前，$A$是最小生成树的子集。在每一步，我们确定可以添加到$A$的边${u,v}$，在不违背这个不变式的情况下，$A\cup \{u，v\}$还是最小生成树的一个子集。

称这样的边为A的安全边（$safe\ edge$），因为它可以在保持不变的情况下添加到$A$。

GENERIC-MST(G,w)
A ← ?
while A does not form a spanning tree
    do find an edge e that is safe for A
        A ← A ∪ e
return A

如何找到安全的边？

定义: 无向图$G=(V,E)$的一个$cut(S,V-S)$是$V$的一个$cut$。

如果一条在$E$中的边$(u, v)$它的一个端点在$S$中，另一个端点在$V-S$中，我们说这条边穿过这个$cut(S,V-S)$

如果$A$中的边没有与该$cut$相交，则该$cut\ respects\ A$的边。

如果边的权值是任何边穿过$cut$的最小值，则边就是穿过$cut$的轻边($light\ edge$)。注意，可以有更多轻边，那么选择其中一条即可。

简单来说，就是$A∪safe\ edge$就是最小生成树的子集，$A$中的点没有穿过$cut$，再在$cut$中找到轻边作为安全边，得到新的$A$，然后再找到新的$cut$，满足$A$没有穿过$cut$，循环此过程，直至找到$n-1$条边。

定理：设$G=(V,E)$是连通的具有权重$w$的无向图，令$A$是$E$的子集，包含在$G$的最小生成树中。设$(S, V-S)$为任意$cut(respect\ A)$，设$(u,v)$为穿过$(S, V-S)$的轻边。那么$(u,v)$是$A$的安全边。

证明:

设$T$是一个最小生成树，包含$A$。

若$T$包含轻边$(u,v)$，则$A\cup \{u，v\} \in T$,
若$T$不包含轻边$(u,v)$，构造另一棵最小生成树$T’$，对于当前生成树$T，u，v$之间没有直接的边相连，但可以通过路径$p$连通，按图中将$G$分割为$cut$两部分，使得$u， v$在$cut$不同的点集，那么必然存在这样的$x，y$也被划分在$cut$两部分，边$(u,v)(x,y)$都穿过该$cut$，$(u,v)$是轻边，连接$(u,v)$，断开$(x,y)$，得到新的生成树$T’$，$T’=T-(x,y)\cup (u,v)$。因为$(u,v)$是一个轻边，$w(u,v)\leq w(x,y)$。因此,$w (T’) = w (T) - w (x, y) + w (u, v) \leq w (T)$。由于$T$是最小生成树，所以$T’$也必须是最小生成树。

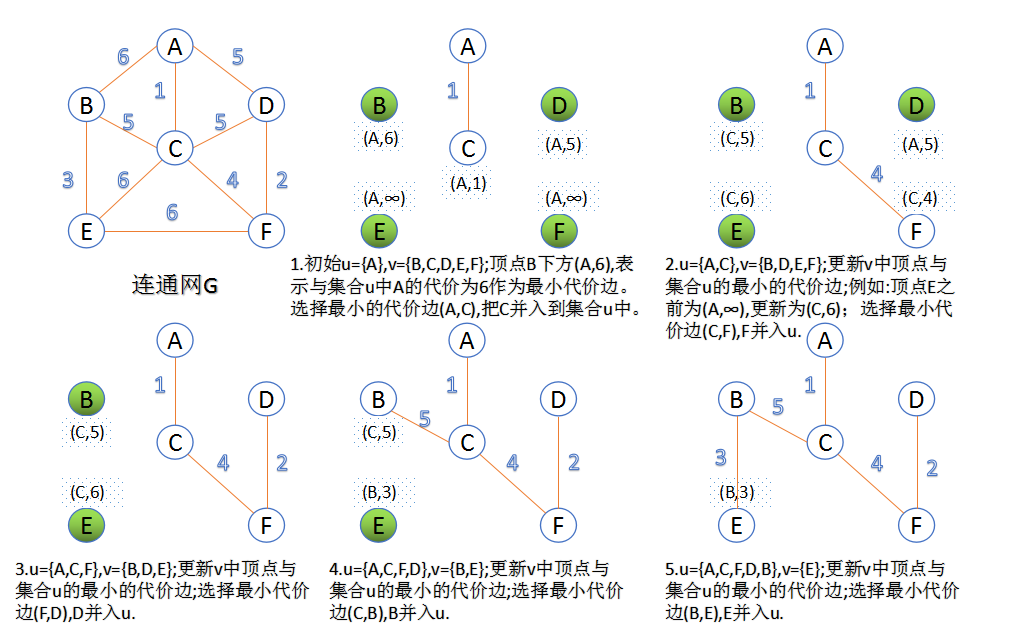
Kruskal , Prim使用特定的规则来确定安全边。

kruaskal算法找到安全边的方法是，在所有连接森林中两颗不同树的边里面，找到权重最小的边$(u,v)$。

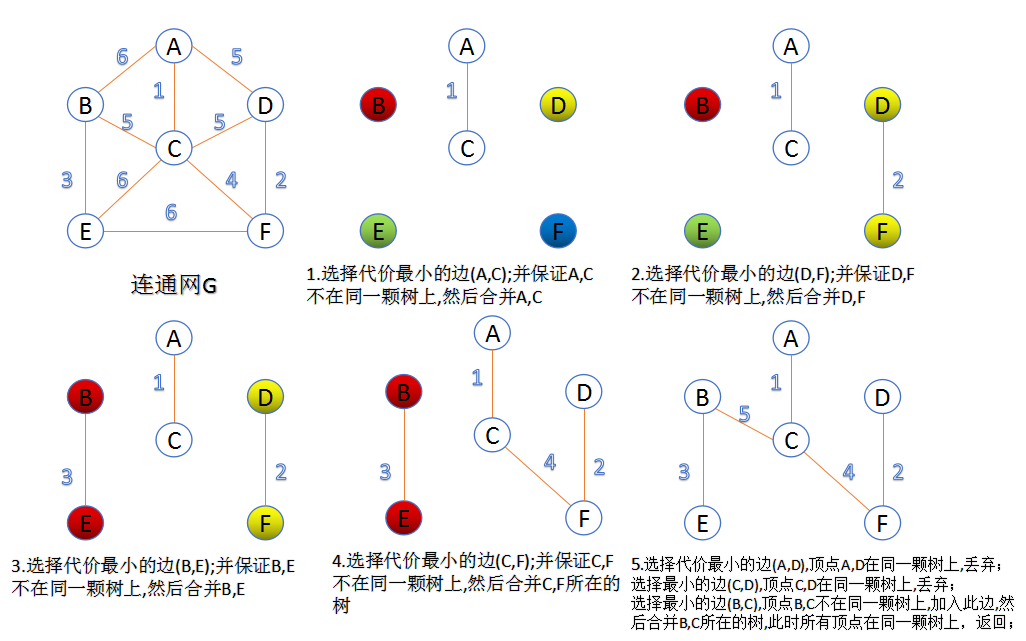
Prim算法所具有的一个性质是集合$A$中边总是构成一棵树。这颗树从一个任意的根节点r开始，一直长大到覆盖$V$中的所有结点时为止。算法每一步在连接集合$A$和$A$之外的节点所有边中，选择一条轻边加入到$A$中。

最大独立集(Maximum independent set)

Greedy independent set
input Graph G=(V,E);
output independent set V' in G;
begin
    V':=ф
    U:=V
    while U is not empty do
    begin
        x: vertex of minimum degree in graph induced by U
        V':=V'U(x);
        eliminate x and all its neighbors from U
    end
    return V'
end

贪心算法找不到最大独立集的例子：

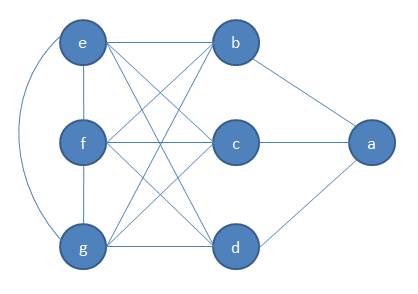
贪心结果：${a, e}$
实际结果：${b, c, d}$

可以看出，随着左部和中部图中点数的增加，贪心所得到的解与最优值可以相差任意远。可以使用图的密度函数判断贪心算法的表现。

定理：假设图$G$有$n$个点和$m$条边，记$\delta =\frac{m}{n}$为图G的密度。贪心算法求得的解$m_{Gr}(G)\geq \frac{n}{(2\delta +1)}$

证明：

设$x_i$为程序while循环第$i$次迭代时选定的顶点，$d_i$为$x_i$的度。
该算法将$x_i$及其所有$d_i$邻居从$G$中删除。第$i$步删除$d_{i+1}$个点，得到

$\sum_{i=1}^{m_{Gr}(G)}(d_i+1)=n.........(1)$

又因为删除点的同时会删除边，那么与$x_i$相连的$d_i$个点至少度是$d_i$，那么删除的边有$(d_i+1)d_i$，又$d_i$个点之间可能存在互相连接的情况，那么删除的边至少有$(di+1)di/2$，删除的边数一定小于总边数，得

$\sum_{i=1}^{m_{Gr}(G)}(d_i+1)\frac{d_i}{2}\leq m=\delta n..........(2)$

$(2)*2+(1)$得

$\sum_{i=1}^{m_{Gr}(G)}(d_i+1)^2\leq n(2\delta +1)$

利用柯西斯瓦格不等式，对于所有的$i$，当$d_i+1=\frac{n}{m_{Gr}(G)}$时，不等式的左边取得极小值。

$n(2\delta +1)\geq \sum_{i=1}^{m_{Gr}(G)}(d_i+1)^2\geq \frac{n^2}{m_{Gr}(G)}$

得证。

下面的定理提供了最优解与贪婪算法求得的解之间的关系。

定理：有$n$个顶点和$m$的图$G$，设$\delta =\frac{m}{n}$。可以找到一个独立的集合$m_{Gr}(G)$，令最优解$\frac{m^*(G)}{m_{Gr}(G)}\leq (\delta +1)$

证明:

本证明与前一证明相似。在本例中，确定一个最大的独立集合${V^}$，令$k_i$为在第$i$次循环中所删除$d_{i+1}$个顶点并在${V^}$中的顶点数。显然

$\sum_{i=1}^{m_{Gr}(G)}k_i=|V^*|=m^*(G)............(3)$

由于贪心算法选择的顶点最小度，删除的顶点的度的和至少是$d_i(d_i+1)$。

因为一条边的两个端点不可能都在$V^$中，*它这样删除边的数目至少为$\frac{(d_i(d_i+1)+k_i(k_i-1))}{2}$，这里可以修改$(2)$，得

$\sum_{i=1}^{m_{Gr}(G)}\frac{d_i(d_i+1+ki(k_i-1))}{2}\leq \delta n...........(4)$

$(2)+(3)+2*(4)$得

$\sum_{i=1}^{m_{Gr}(G)}((d_i+1)^2+k_i^2)\leq n(2\delta +1)+m^*(G)$

应用$C-S$不等式，当$d_i+1=\frac{n}{m_{Gr}(G)}\ and\ k_i=\frac{m^*(G)}{m_{Gr}(G)}$，上述不等式左边最小，因此

$n(2\delta +1)+m^*(G)\geq \sum_{i=1}^{m_{Gr}(G)}((d_i+1)^2+k_i^2)\geq \frac{n^2+m^*(G)^2}{m_{Gr}(G)}$

即

$m_{Gr}(G)\geq m^*(G)\frac{\frac{n}{m^*(G)}+\frac{m^*(G)}{n}}{2\delta +1+\frac{m^*(G)}{n}}$

当$m^*(G)=n$时，不等式最小。把这一项代入，定理成立。

背包问题(Greedy knapsack)

输入:集合$X$的$n$个元素，对于$X$中的每个$x_i$，价值$p_i$，重量$w_i$，正整数$b$；
输出:子集$Y\in X$使得$\sum_{x_i\in Y}w_i\leq b,max\ {\sum_{x_i\in Y}} p_i$
按$\frac{p_i}{w_i}$的规则进行贪心选择。

begin
    sort X in non-increasing order with respect to the ratio pi/wi;
    Y:=empty set;
    for i=1 to n do
    if b>=wi then
    begin
        Y=YU{xi}
        b=b-wi
    end
    return Y
end

找不到最优解的例子：
令$p_i=w_i=1，i=1,2，..，n-1, p_n=b-1, w_n=b=k_n$，其中$k$是一个任意大的数。
在这种情况下，最优解$m^*(x)=b-1$;而贪心算法找到的解的值为$n-1$。因此

$\frac{m^*(x)}{m_{Gr}(x)} > k$

贪心算法的劣势是由于算法没有将价值最高的元素包含在解中，而最优的元素正是价值最高的。这表明一个简单的修改贪心的程序有更好的性能。

定理：给定一个背包的实例$x$，令$m_H(x)=max(P_{max}，m_{Gr}(x))$，其中$P_{max}$是$x$中一个项目的最大价值，$m_H(x)$满足以下不等式:$\frac{m^*(x)}{m_H(x)}< 2$。

证明：设$j$为根据贪心选择第一个装不进背包物品的下标，此时背包转装入的物品价值为

$\overline{p_j}=\sum_{i=1}^{j-1}\leq m_{Gr}(x)$

重量为

$\overline{w_j}=\sum_{i=1}^{j-1}w_i\leq b$

首先证明任何最优解必须满足以下条件不等式:
$m^*(x)<\overline{p_j}+p_j$，

因为装入前j-1个物品后，容量还剩余$b-\overline{w_j}< w_j$，贪心选择在装入$j-1$个物品后，无法装入$j$，其密度为$\frac{p_j}{w_j}$，那么如果剩余容量按最优的去放，$(b-\overline{w_j})\frac{p_j}{w_j}<w_j\frac{p_j}{w_j}=p_j$

如果$p_j<\overline{p_j}$，那么$m^*(x)<2\overline{p_j}\leq 2m_{Gr}(x)\leq 2m_H(x)$；

如果$p_j>\overline{p_j}$，那么$P_{max}>\overline{P_j}$，有$m^*(x)\leq \overline{p_j}+p_j\leq 2{p_j}\leq 2P{max}\leq 2m_H(x)$

The Stein-Lovasz Theorem

The stein-lovasz Theorem 理论最基本的模型是解决集合的元素覆盖问题。使用贪心算法，以获得一个使用最少列元完成最大行覆盖的方案。
假设$(0,1)$矩阵$A$的大小是$N×M$ ,矩阵$A$的特征是每行至少具有$v$个$1$，每列最多$a$个$1$。假设现在从其中抽取一个子矩阵$C⊂A$,大小是$N×K$，使得子矩阵的每行元素都不是全零行，证明$K$存在一个上界，
$K≤\frac{N}{a}+(\frac{M}{v})lna≤(\frac{M}{v})(1+lna)$
分析：能不能使用一种抽取列数尽可能少的方案，如果使用的列数目比给定的边界条件$\frac{N}{a}+(\frac{M}{v})lna$小，那么原来的问题就自然获得证明。

贪心算法思路描述如下

初始化矩阵$(0,1)$矩阵$A$，每列的$1$权重值$c_i∈\{1,2,3,……,a\}$,然后按照列权重按照 $a,a-1,a-2,…,1$ 执行降序排序，此时的矩阵命名为$A_a$;
从最左边权重最高为$a$的第一列开始，删除这一列，并且这列对应的$1$所在相应的$a$个行也统一删掉。在删除$1$列和$a$行后的矩阵$A$，重新划定权重，继续寻找左边最高权重为$a$的列，继续删除。在删除$2$列和$2∗a$行后的矩阵$A$，重新划定权重，继续寻找左边最高权重为$a$的列，继续删除。重复$K_a$次后，把最高权重为$a$的列及对应的$a∗K_a$行都删掉了，此时的矩阵变成了$A_{a−1}$;
以矩阵$A_{a−1}$开始，从左边权重最高为$a-1$的第一列开始，删除这一列，并且这列所对应的$a−1$行也统一删掉。删完后，重新划定权重，继续寻找左边最高权重为$a-1$的列，继续删除。重复$K_{a−1}$次后，把最高权重为$a-1$的列及其对应的$(a−1)∗K_{a−1}$行都删掉了，此时的矩阵变成了$A_{a−2}$.
重复步骤3，删除权重为$a-2,a-3,…,1$的列，直到矩阵$A_1$变成了空。
将之前删除的所有列元集中起来重新组合成$N×K$矩阵，$K=\sum_{i=1}^a K_i$

证明：

假设$A_a=A_{N*M}$表示由$a$个1且每列的1互不重合的列组成的矩阵

$A_{a-1}’$表示由a-1个1且每列的1互不重合的列组成的矩阵。$|A_a’|=K_a$，那么删除覆盖的$K_a\cdot a$行得到新的矩阵$A_{a-1}=A_{(N-aK_a)\times (M-K_a)}$，那么每一列至多有$a-1$个$1$，

$|A_{a-1}’|=K_{a-1}$，那么删除覆盖的$K_{a-1}\cdot (a-1)$行得到新的矩阵$A_{a-2}$。

以此类推，$A_{i-1}$，每行至少$v$个1，每列至多$i-1$个$1$，那么有$N-aK_a-(a-1)K_{a-1}-…-iK_i$行，记为$k_i$行，有$M-K_a-…-K_i$列。

$k_a=N-aK_a$，即$K_a=\frac{N-k_a}{a}$，令$N=k_{a+1}$，则$K_a=\frac{k_{a+1}-k_a}{a}$，以此类推得到

$K_i=\frac{k_{i+1}-k_i}{i}$ $\sum_{i=1}^{a}K_i=\sum_{i=1}^{a}\frac{k_{i+1}-k}{i}=\frac{k_{a+1}}{a}-\frac{k_a}{a}+\frac{k_a}{a-1}-\frac{k_{a-1}}{a-1} +...+\frac{k_2}{1}=\frac{N}{a}+\frac{k_a}{a(a-1)}+\frac{k_{a-1}}{(a-1)(a-2)}+...+\frac{k_2}{2\times 1}$

使用双计数，分别对行和列进行计数，对于$A_{i-1}$，每一行至少$v$个1，而每列至多$i-1$个$1$，可得对$1$进行行计数不会超过进行列计数，即

$k_i\times v\leq (M-K_a-...-K_i)\times (i-1)\leq M\times (i-1) \frac{k_i}{i-1}\leq \frac{M}{v}$

那么

$\sum_{i=1}^{a}K_i\leq \frac{N}{a}+\frac{1}{a}\frac{M}{v}+\frac{1}{a-1}\frac{M}{v}+...+\frac{1}{2}\frac{M}{v}=\frac{N}{a}+\frac{M}{v}(\frac{1}{a}+\frac{1}{a-1}+...+\frac{1}{2})\leq \frac{N}{a}+\frac{M}{v}lna\leq \frac{M}{v}+\frac{M}{v}lna=\frac{M}{v}(1+lna)$

应用1：完美哈希族函数（Perfect Hash Function）

$(n,m,w)$-完美哈希族是一个函数F集合，使得$|Y|=n$， $|X|=m$,
$f:Y\rightarrow X$对于$F$中的每一个$f$，对于任何$C\subseteq \{1,2,…,n\}$使得$|C|=w$，$C$是$Y$的$w$元子集合，并且至少存在一个$F$中的$f$使得$f|C$是一一对应的。如果$|F|=N$那么完美哈希族可以记作$PHF(N;n,m,w)$。
求满足条件的函数数目的一个上界。

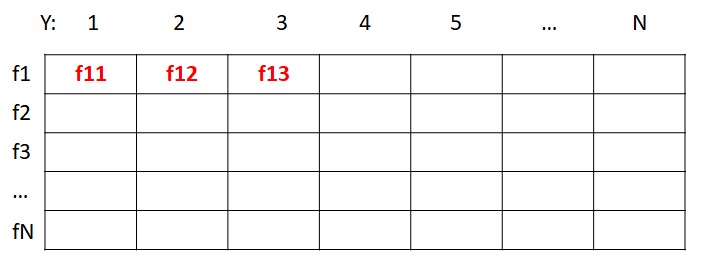
$|F|=N$，如上图，假设$w=3$，那么任选$Y$中的三列，有$\binom{n}{3}$种选择，要求其中存在一行使得三个函数值各不同，例如取$1，2，3$列，$f_{11}$，$f_{12}$，$f_{13}$互不相同就满足要求一一映射。
$f:Y\rightarrow X$，$n$个$Y$对应到$m$个$X$，每一个$Y$有$m$种选择，那么有$m^n$个函数。从中挑出最少的函数(即N越小越好)使得对于任何的$C$可以满足一一对应要求。

套用ST定理：
$N:\binom{n}{w}$，从$M:m^n$个函数中挑选出最少的函数满足要求，那么得到的矩阵就是$NxM$的$(0,1)$矩阵$A$，$A_{ij}=1$的含义就是当$|w|=i$，$f_j$是可以满足一一映射要求的。

$v:\binom{m}{w}w!\cdot m^{n-w}$，表示从$m$个值中选取$w$的值排列放入选择的$w$个，剩余未赋值的$n-w$个，就任意赋值。
$a:\binom{n}{w}$，每一个函数至多覆盖$a$个。

套用S-T定理得

$N\leq \frac{m}{w!\binom{m}{w}}(1+log\binom{n}{w})$

使用概率方法:
从$m^n$个函数中随机选择$N$个函数出来，构造一张随机的函数表，考虑坏概率，在函数表中没有一个函数可以使$w$存在一一映射关系，对于一个函数坏概率为存在一一对应关系的对立事件，取出$N$个函数，得 $(1-\frac{\binom{m}{w}w!m^(n-w)}{m^n})^N\binom{n}{w}$ 使其小于1，那么一定存在完美哈希族。(两边取对数求解)

应用2：分割系统(Splitting Systems)

在某个域中，$\alpha ^n=\beta$，$\alpha ,\beta$已知且为离散的，那么如何求解$n$？

分割系统的提出就是为了解决离散对数问题。

假设$n,t$为偶数，$X$是点集合,$B$是超边集合。
a) $|X|=n$,$B$是$X$的$\frac{n}{2}$子集的集合，称为区组
b)对于每一个$Y\subseteq X$中存在区组$B$，使得$|B\cap Y|=\frac{t}{2}$。
取最少$N$个$B$使得上面的条件满足。

使用S-T定理
$N:\binom{n}{t}$，对所有的t元子集合进行分割;
$M:\binom{n}{\frac{n}{2} }$，完成的方法总数;

接下来确定$v$，那么对于某一行有多少$\frac{n}{2}$元子集合可以分割$t_i$，$t$个位置中一半放$1$，剩余一半放$0$，问题是一个$n$元集合，此时还剩$n-t$个位置没有放数，且还缺少$\frac{n-t}{2}$个1，那么得到子集合个数$\binom{t}{ \frac{t}{2} }\cdot \binom{n-t}{\frac{n-t}{2}}$；

确定$a$，对于固定的$\frac{n}{2}$元子集合可以分割多少$t$，$\binom{\frac{n}{2}}{\frac{t}{2}}\binom{\frac{n}{2}}{\frac{t}{2}}$，套用S-T定理，

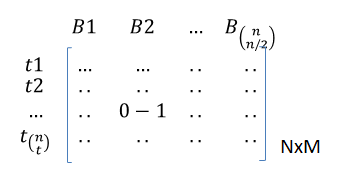
$N\leq \frac{\binom{n}{\frac{n}{2}}}{\binom{t}{\frac{t}{2}}\binom{n-t}{\frac{n-t}{2}}}(1+2ln\binom{\frac{n}{2}}{\frac{t}{2}})$

使用概率方法：
定义$A_i$，第$i$个$t$元子集合未被分割。对于一个$t$元集合没有分割的概率是分割时间的对立事件，为 $1-\frac{\binom{t}{\frac{t}{2}}\binom{n-t}{\frac{n-t}{2}}}{\binom{n}{\frac{n}{2}}}$ 共有$N$个$\frac{n}{2} $元子集合未被分割，为 $(1-\frac{\binom{t}{\frac{t}{2}}\binom{n-t}{\frac{n-t}{2}}}{\binom{n}{\frac{n}{2} }})^N=P(A_i)$ 那么至少有一个$t$元集合未被分割的概率为 $P(\cup A_i)\leq \sum P(A_i)=\binom{n}{t}P(A_i)<1$ 令其小于$1$，那么没有未被分割的情况概率大于$0$。

参考：图论学习笔记五贪心算法 | 码农家园 (codenong.com)