大量数据存储中,在查找的背景下,BST由于树深度过大而造成磁盘IO读写过于频繁,进而导致效率低下。那么如何减少树的深度?
why?
二叉排序树在多数情况能够达到预期的查找效率,但是每个节点只能存储一个元素和只能有两个孩子,大量数据情况下会造成树的深度特别大,查找时多次的访问会造成查找效率的下降。所以引入新的数据结构——多路查找树。
- 多路查找树的每一个节点的孩子树可以多于两个,且每个节点处可以存储多个元素。
- 多路查找树是一种特殊的查找树,所以其元素之间存在某种特定的排序关系。
- 四种特殊形式:2-3树,2-3-4树,B树(B-树),B+树
B树(B-树)
B树(B-树)是一种平衡的多路查找树。2-3树和2-3-4树都是B树的特例。节点的最大孩子数目称为B树的阶(order),因此,2-3树是3阶B树,2-3-4树是4阶B树。
2-3树
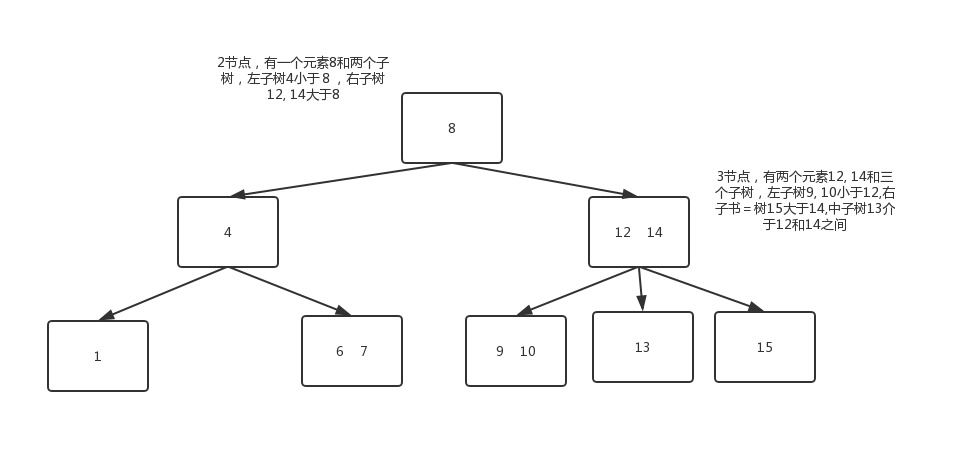
定义2-3树中每一个节点都具有两个孩子(称2节点)或三个孩子(称3节点)。
- 一个2节点包含一个元素(关键字)和两个孩子(只能包含两个孩子或没有孩子),且与二叉排序树类似,左子树包含的元素小于该元素,右子树包含的元素大于该元素。
- 一个3节点包含一小一大两个元素和三个孩子(只能包含三个孩子或没有孩子)。如果某个3节点有孩子,左子树包含小于较小元素的元素,右子树包含大于较大元素的元素,中间子树包含介于两元素之间的元素。
2-3树的所有叶子都在同一层次。
插入/删除:略
2-3-4树
2-3-4树是2-3树的扩展,包括了4节点的使用,一个4节点包含小中大三个元素和四个孩子(或没有孩子)。
插入/删除:略
应用:内外存的数据交互
计算机存储设备一般分为两种:内存储器和外存储器。 操作系统经常与内存和硬盘这两种存储设备进行通信,与内存操作,是虚拟一个页的概念来作为最小单位。
内存储器为内存,内存存取速度快,但容量小,价格昂贵,而且不能长期保存数据(在不通电情况下数据会消失)。
外存储器即为磁盘读取,磁盘读取数据靠的是机械运动,每次读取数据花费的时间可以分为寻道时间、旋转延迟、传输时间三个部分。
寻道时间指的是磁臂移动到指定磁道所需要的时间,主流磁盘一般在5ms以下;旋转延迟就是我们经常听说的磁盘转速,比如一个磁盘7200转,表示每分钟能转7200次,也就是说1秒钟能转120次,旋转延迟就是1/120/2 = 4.17ms;传输时间指的是从磁盘读出或将数据写入磁盘的时间,一般在零点几毫秒,相对于前两个时间可以忽略不计。那么访问一次磁盘的时间,即一次磁盘IO的时间约等于5+4.17 = 9ms左右。执行一次IO的时间可以执行40万条指令,所以磁盘IO是非常高昂的操作。
当要处理的数据很大时,无法一次全部装入内存。这时对B树调整,使得B树的阶数与硬盘存储的页面大小相匹配。比如说一棵B树的阶为1001(即1个节点包含1000个关键字),高度为2(从0开始),它可以存储超过10亿个关键字(1001x1001x1000+1001x1000+1000),只要让根节点持久的保留在内存中,那么在这颗树上,寻找某一个关键字至多需要两次硬盘的读取即可。
查询
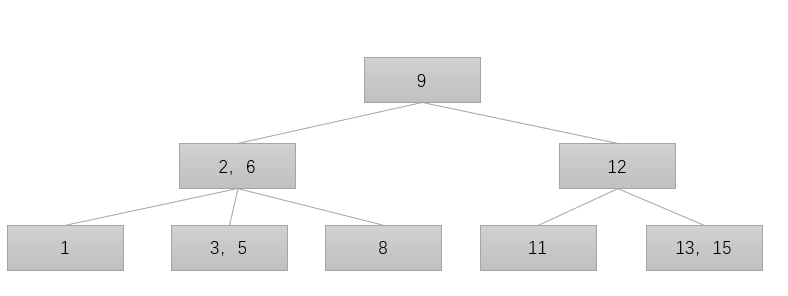
假设要查询的数值是5,查询过程:
第一次IO:把9节点加载到内存中,在内存中与目标比较;
第二次IO:把(2,6)节点加载到内存中,在内存中与目标比较;
第二次IO:把(3,5)节点加载到内存中,在内存中与目标比较;
二叉查找树情况下,每个节点只存放一个数据,查询数据的时候每加载节点比较一遍,进行一次磁盘IO。最坏情况下,磁盘IO次数等于树的高度
B树在查询过程中比较次数其实并不会比二叉查找树少,尤其当某一个节点中的元素数量很多的时候。可是,单个节点的元素比较都在内存中进行,相比较于磁盘IO的速度,内存中比较耗时可以忽略不计,性能提高比较大。所以只要树的高度足够低,IO数量足够少,查询性能提升越明显。 相比之下,只要不超过磁盘页的大小,仅仅是多了几次内存的交互,这也是B树的优势之一。
B树应用于文件系统索引和部分非关系型数据库,如MongoDB
B+树
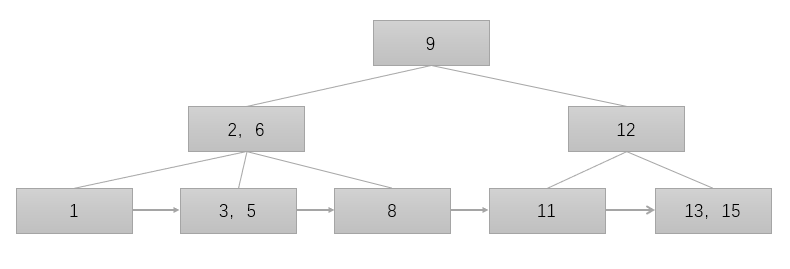
查询
单元素查询过程:在单元素查询时,B+树会自顶向下逐层查找节点,最终找到匹配的叶子节点。
范围查询过程:例如查询3到11之间的元素,首先单元素查找到下限3,然后在链表上做遍历即可
3, 5 -> 8 -> 11
B树只能依靠中序遍历来实现范围查询,3, 5 (-> 6) -> 8 (->9) -> 11
B+树适合随机查找,只不过查到后是索引,不能提供实际记录的访问,还需要到达包含此关键字的终端节点。非叶结点仅具有索引作用,跟记录有关的信息均存放在叶结点中。B+树还适合带有范围的查找。
和B树查询的不同
- B+树的中间节点没有卫星数据。B树中所有节点都带有卫星数据,而在B+树中,只有叶子节点带有卫星数据,其余中间节点仅仅是索引,没有任何的数据关联。所以同样大小的磁盘页可以容纳更多的节点元素,也意味着数据量相同的情况下,B+树的结构比B树更加“矮胖”,因此查询IO次数更少;
- B+树的查询必须最终找到叶子节点,而B树只要匹配到元素即可,不论它是中间节点还是叶子节点,因此B树的查询性能并不稳定(最好情况是只查询根节点,最坏情况查询到叶子节点),而B+树每一次查找都是稳定的。
卫星数据:指索引元素所指向的数据记录,比如数据库中的某一行
应用
大部分关系型数据库(如MySQL)使用的都是B+树作为索引。
关于索引
- 磁盘IO的存取次数是评价一个数据库索引优劣的关键性指标。利用索引查询数据的时会逐一加载磁盘页到内存当中,每一页对应索引树的节点。所以索引需要的是减少磁盘IO的次数以及节点存储更多的数据量。
- 在数据库的设计中,聚集索引(Clustered Index),叶子节点直接包含了卫星数据。在非聚集索引(NonClustered Index),叶子节点叶子节点存储的是主键值。
B+树相较于B树的优势有三个:
- IO次数更少:单一节点比B树存储了更多的数据,使得查询IO的次数减少
- 查询性能稳定:所有查询都要查找到叶子节点,查询性能稳定
- 范围查询简便:所有叶子节点形成有序链表,便于范围查询