双计数狭义上讲,对于一个集合运用两种不同的方式(行 / 列),得到等式结果或者不等式的结果。
握手定理
对于图$G=(V, E)$,有
证明:对图G的邻接矩阵中1的个数分别从行(左),列(右)进行计数。即对二元组$\{(v,e)|v\in e\}$进行计数。
推论:图中奇度点数目为偶数。
超图握手定理:对于超图$G=(V, B)$
完全图边的双计数
对于一个完全图,共有$n\choose 2$条边;
将完全图划分为$S$部分,每部分有$n_i$个点,${n_i \choose 2}$条边;
每部分之间有$n_in_j$条边。
等式证明
证明:设$A$为$k$元子集,对二元组$\{(x,A)|x\in A, |A| = k\}$进行计数。
证明:设$A$为$k$元子集,$k=1,2,…,n$,对二元组$\{(x,A)|x\in A, |A| = k\}$进行计数。
证明:设$A$为$l$元子集,$B$为$k$元子集,对二元组$\{(A,B)||A|=l,|B|=k,A\subseteq B\}$进行计数。
Turan Number
图兰数$T(n,k,l) (l\leq k \leq n)$是$n$元集合$X$的$l$元子集的最小值(下界),使得$X$的每个$k$元子集至少包含一个这样的l元子集。
证明:设$F$为满足条件的l元子集,记$F=\{A_1,A_2,…\}$,此时可用关联矩阵表示,$A_i$为满足条件的$l$元集合,$B_i$为$ k$元子集,若$A_i$在$B_i$上,则为$1$,就可以得到一个$0-1$矩阵。对矩阵中$1$的个数计数。
行计数:对于某一个$l$元集合,有$\binom{n-l}{k-l}]$个$k$元集合包含它,共有$|F|$个,行计数$1$的个数为$|F|\binom{n-l}{k-l}$
列计数:每个$B_i$必包含一个$A_i$,则每一列至少有一个$1$,可以得到$|F|\binom{n-l}{k-l} \geq {n\choose k}$
Zarankiewicz’s problem
对于一个$n\times n$的$0-1$矩阵,如果不存在$a\times a$的全$1$子矩阵,那么这个$nxn$的矩阵最多有多少个1?
等价于:用二部图重新表述这个问题。一个部分大小为$n$的二部图$G=(V_1,V_2,E)$,其中$V_1,V_2$是顶点的不相交$n$元集合,$E\in V_1\times V_2$是边的集合。令$K_a(n)$为最小整数$k$边,使得任意大小为$n$且边数大于k的二部图至少包含一个$a\times a-clique$。对于任意的自然数$n$和$a$,
对$S= \{(x,A)|x\in V_1,A \in V_2,|A|=a,且x与A中所有点都有边相连\}$计数, 即对下图中的结构进行计数。
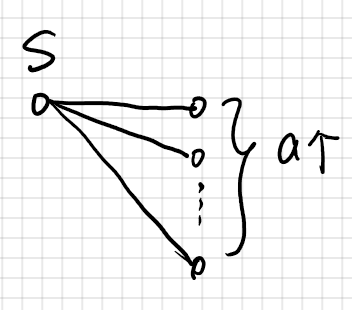
固定$x$:从与$x$相连的元素中取$A$,设$x$的neighbor为$d(x)$,那么A有$\sum_{x\in V_1}\binom{d(x)}{a}$种选法,且$|S|=\sum_{x\in V_1}\binom{d(x)}{a}$
固定$A$:从$n$中选出$a$元集合,与之对应相连的$x$最多有$(a-1)$个,否则就会出现$a\times a-clique$,即$|S| \leq \binom{n}{a}(a-1)$
即$\sum_{x\in V_1}\binom{d(x)}{a}\leq \binom{n}{a}(a-1)$
Jensen不等式,对凸函数有:
Jensen不等式可由数学归纳法证明,略。
令$f(x)=\binom{x}{a}$,$x_i=d(x_i)$;
根据Jensen不等式,有
$\frac{1}{n}\sum_{x\in V_1}\binom{d(x)}{a}\geq \binom{\frac{1}{n}\sum_{x\in V_1}d(x)}{a}$
$\sum_{x\in V_1}\binom{d(x)}{a}\geq n\binom{\frac{1}{n}\sum_{x\in V_1}d(x)}{a}=n\binom{\frac{|E|}{n} }{a}$(因为为二部图,则degree为一倍边数)
即$n\binom{\frac{|E|}{n} }{a}\leq \binom{n}{a}(a-1)$
经过放缩有$n(\frac{|E|}{n}-(a-1))^a<\frac{n(|E|/n)(|E|/n-1)…(|E|/n-(a-1))}{a!}=n\binom{\frac{|E|}{n} }{a}$
$\binom{n}{a}(a-1)=\frac{n(n-1)…(n-(a-1))}{a!}(a-1)<\frac{n^a}{a!}(a-1)$,两边同时开a次方即可解。
- $K_a(n)$的下界可以用概率方法求得
H-free图
一个有$n$个顶点的无$H$图可以最多有多少条边?
定理:如果图$G=(V,E)$中不包含4个点的圈, 即$C_4-free$,那么有$|E|\leq \left \lfloor n/4(1+\sqrt{4n-3}) \right \rfloor$
令点集$V={1,2,…,n}$,用于双计数的集合为$S=\{(u,\{v,w\})|u与v,w都邻接,且v≠w\}$,即对下图中的结构进行计数。

固定$u$,那么$v$和$w$只能在度为$d(u)$的点中选取,即$\binom{d(u)}{2}$,有$\sum _{u\in V}\binom{d(u)}{2}=|S|$;
固定$v$和$w$,最多只有一个点可以和它们都关联,那么有$\binom{n}{2}\geq |S|$,
那么,$\sum _{u\in V}d^2(u)\leq \sum _{u\in V}d(u)+n(n-1)$,
柯西—施瓦茨不等式,$|(\alpha ,\beta )|\leq ||\alpha ||*||\beta ||$
上述不等式中对应的分别是$[d(u_1),d(u_2)….d(u_n)]$,$(1,1,…1)$。
由柯西—施瓦茨不等式得,$n\sum_{u\in V}d^2(n)\geq (\sum_{u\in V}d(n)*1)^2$,代入上式,$\frac{(\sum_{u\in V} d(u))^2}{n}\leq \sum_{u\in V}d(u)+n)n-1$,
由握手定理得$4|E|^2\leq n2|E|+n^2(n-1)$,求解n可得上述结论。
三计数
在超图中,有
对于集合$(X,F)$,$X$为点集合,$F$为超边集合,对三元组${(x,A,B)|A,B∈F,x∈A,x∈B}$计数。
左:$x$在全集$X$上,$A,B$集合均包含点$x$;
中:先选出在$A$的$x$,再使得$x$在$B$中;
右:先选出$A$和$B$集合,使得$x$在$A$和$B$上,即在$A\cap B$上。
整除关系
假设两个有限集$R$和$C$和一个子集$S\subseteq R\times C$。无论何时$(p,g)∈s $那么认为$p$和$q$是关联的。
设$r_p$表示$p$固定,与$p$关联的元素数目;$c_p$表示$q$固定,与$q$关联的元素数目。有
假设$M_{|p|\times |q|}$的关联矩阵使用双计数进行证明,矩阵中若$p_i$和$q_j$相关联,$a_{ij}$则置为$1$,否则为$0$,那么$|S|$就是矩阵$M$中全部$1$的个数,等式的第一项可从行计数,最后一项可从列计数角度统计矩阵中1的个数。
例:
$R=C={1,2,…,n}$,集合$S=\{(i,j)|i可以整除j\}$,
$t(j)$表示$j$的因子的数目,如$j=4$,因子有$1,2,4$,那么$t(4)=3$。
| i/j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 1 | ||||
| 3 | 1 | 1 | ||||||
| 4 | 1 | 1 | ||||||
| 5 | 1 | |||||||
| 6 | 1 | |||||||
| 7 | 1 | |||||||
| 8 | 1 |
Sperner Lemma
假设某个顶点为$V1、V2、V3$的“大”三角形被三角化了(也就是说,被分解成有限数量的“小”三角形,这些“小”三角形每条边都能拼接在一起)。
假设三角化中的顶点从集合$\{1,2,3\}$中获取颜色,使得$V_i$接收颜色$i$(对于每个$i$),并且沿着$V_i$到$V_i$的边的顶点只用$i$和$j$的颜色,而内部顶点用1、2或3的颜色任意着色。那么在三角测量中一定有一个小的“三色”三角形。
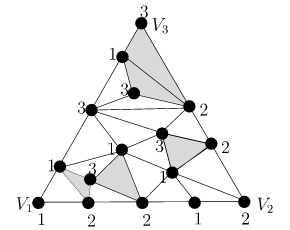
证明:
假定大三角形外部有一点$A$,每一个小三角形中心都有一个顶点$O$,若小三角形含有1,2顶点,则从$O$经过1,2点构成的边形成一条边(即出度),如下图
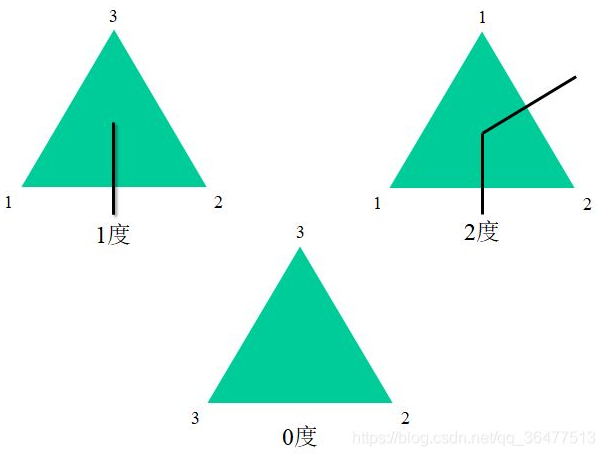
根据握手定理可知,度之和必为偶数, 在$V_1$和$V_2$构成的边上,观察可得出度必为奇数,即边上(1,2).(2,1)的线段必有奇数个,那么在小三角形必存在奇数度的三角形,即必存在1度的三角形,得证。